개념-quaternion

c code

Quaternion, Euler, Matrix변환

필수x100 시청영상

아래 영상은 Quaternion은 complex를 확장한 것이고,
Quaternion에 unit quaternion을 곱하는 것은 4d hypersphere의 회전임을 직관적으로 설명하는 3Blue1Brown의 감동적인 영상이다.
Visualizing quaternions (4d numbers) with stereographic projection Quaternions and 3d rotation, explained interactively
quaternions simulation

개요

mujoco를 통해 biper의 다리회전을 구현하다가 로보틱스에서는 회전을 quaternion으로 표현하는게 많은 이득이 있다고 한다.(gimbal lock해결)
위키피디아에서 Quaternion에 대해 알아보았다.
Quaternion이 SO(3)에 속하는, 회전행렬과 동치라는 것 말고는 이해가 안된다.. lie group과 마찬가지로 추상대수학에 대한 이해가 필요해보인다.
3차원 회전 연산(rotation operation)만 보면, 사원수의 회전 표현식이 벡터나 행렬 공식보다 확실히 아름답다고한다.

문제상황

1. 우선 Quaternion이 뭔지 직관적으로 모르겠다.
2. c codeQuaternion, Euler, Matrix변환이 이해가 안된다.

해결방법

1. 부족한 직관을 채우기위해 유튜브에서 3Blue1Brown이 제작한 Visualizing quaternions (4d numbers) with stereographic projection을 참고했다.
2. 회전에 대응되는 Quaternion number 계산방법을 알아보기위해 Using quaternions as rotations을 참고했다.

1.2. Quaternion에 대한 이해

quaternion은 real quaternion와 vector quaternion(i,j,k)으로 나뉜다.
\({\displaystyle a+b\ \mathbf {i} +c\ \mathbf {j} +d\ \mathbf {k} ,}\)

quaternion에 unit quaternion을 곱하는 행위는 4d hyper sphere를 회전시키는 것이다..!
(정확히는 동기화된 서로 직교하는 두 원의 2d회전. 한 원이 회전하는 양만큼 직교하는 다른 원도 회전한다.)
unit quaternion를 나타내는 모든 좌표 상의 임의의 점은 회전으로 생각할 수 있고, 그 모든 점(회전)은 3d로 mapping할 수 있다.

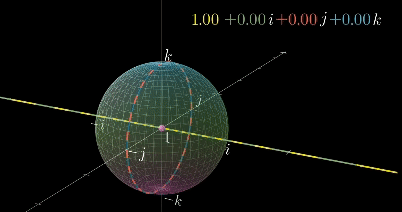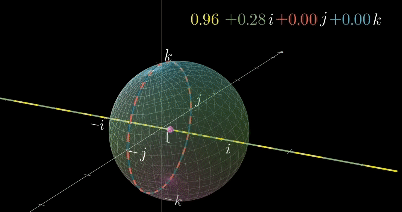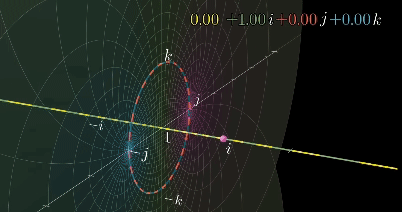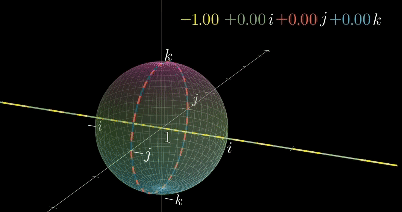
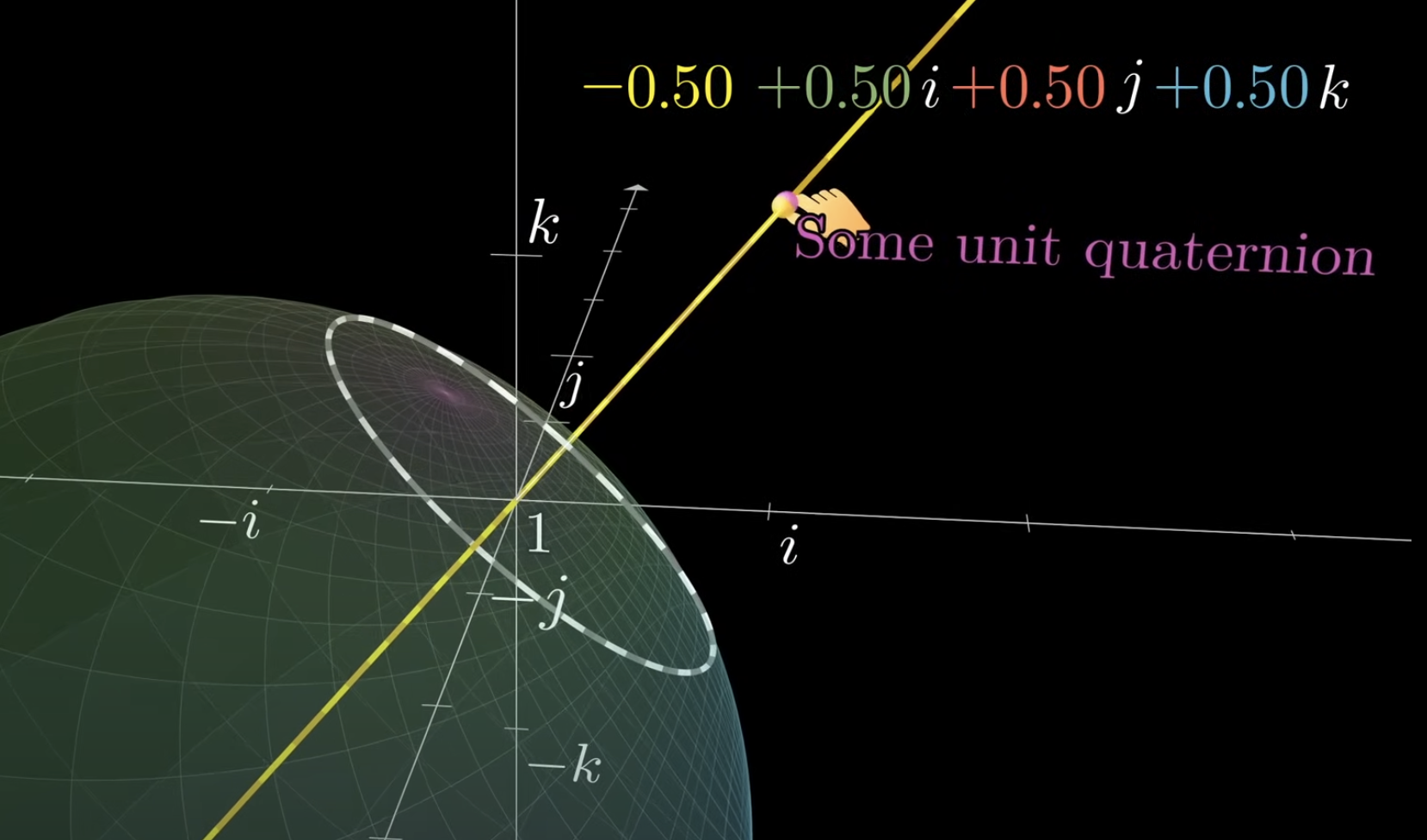
아래 영상과 같이, 초기에 real part가 0이라서 vector space(ijk)에 unit sphere로 표시되는 4d hypersphere는
우측상단에 표기되는 unit quaternion을 곱할 때, 우리가 인지할 수 없는 방식으로 회전하게된다.
해당 경우 pure한 i축 성분을 곱하고 있으므로 i축에 대한 회전이다.
회전의 결과는 역시 unit quaternion를 나타내는 모든 좌표 상의 임의의 점으로 나타난다.

영상의 결과에 대해 해석해보자.
해당 vector space(ijk)에서 회전의 결과인 점들의 이동을 살펴보면, i를 곱할 때마다 다음과 같은 일이 벌어진다.
jk평면에 mapping한 경우: i축기준으로 반시계로 90도 회전
jk평면과 수직한 평면(real,i평면)에 mapping한 경우:
해당 공간에서 real축을 인지할 수는 없지만, 2d에서 회전에 해당하는 2d circle을 1d line에 mapping할 수 있었던 것처럼,
(real,i축에 수직한 축 기준으로 회전의 결과를 i축에 나타내는 방법. 이를 i축에 대한 회전이라고 하자. 이게 핵심임.
허수축은 방향만을위해 존재하는 것이지 대소비교는 의미없으므로 이런짓이 가능함. 회전의 결과를 i축 여러군데에 표시하는 거임.)
4d hypersphere이 i축을 지나는 교점만큼은 mapping을 통해 인지할 수 있다.
따라서 i축의 1d line을 따라 1,i,-1,-i(실제 대소비교가 불가능하지만 2d를 1d로 projection하면 이러한 순서임)순서로 반복하는 각 현상은
{real,i}평면에서 2d circle을 따라 {real축,i축}에 수직한 축기준으로 90도 회전하는 현상이 일어났고 이를 i축에 projection한 것이라고 상상할 수 있다.
즉 i축기준회전이라는 말은 사실 {i,j,k,real}모든 축에 대한 회전이고, 우리는 real축을 인지할 수 없기때문에
이를 i축에 projection함으로써, i축에 회전량이 기록되고, quaternion number로 표기되는 것임.

정리하자면 순수한 회전이라는 말은, unit quternion number를 곱한다는 말이고,
이 경우 곱해지는 quternion number를 구성하는 성분 중에 real quternion의 인지를 포기하고 vector quternion을 basis로 하는 space에
real number -1에서 바라보는 방향으로 quternion number를 projection할 경우,
각 축에는 real축과 그 축에 수직인 축에 대한 회전량이 저장되어 있기때문에
곱해진 결과인 quternion number를 통해 각 축에 대한 회전량을 알 수 있게 된다.
(i축에는 i와 real에 수직인 축에 대한 회전,j축에는 j와 real에 수직인 축에 대한 회전,k축에는 k와 real에 수직인 축에 대한 회전)
즉 다음과 같이 임의의 unit quaternion을 곱하게 될 때, 이에 수직하고 vector space의 원점(1+0i+0j+0k)을 지나는 평면은 vector quaternion의 크기만큼 회전(최대 1 radian이므로 90degree)하게 된다.
(이 때 회전축은 {real,i,j,k}에 모두 수직인 방향으로의 hyper sphere의 회전이고, 인지할 수 없는 orthogonal한 세축에 대해 \(\sin(\theta)\)만큼 projection되기때문에, 그러므로 각 basis에 대해 모두 수직인 방향으로 회전이 일어나는 것이고, 각각에 projection될 수 있기때문에 그 합은 vector quaternion의 크기와 같다.)

이는 3차원의 회전을 기술하기 위한 것으로, 4차원 hyper sphere를 회전시키고 real축의 인지를 포기하면 3축(i,j,k축은 아닌 어떤 축)에 대한 회전량을 알 수 있게 되는 놀라운 계산법인 것이다..

1.2. 주의할 점

quternion number는 complex number의 확장인만큼, commutativity(교환성)가 성립하지 않는다.
실수의 경우 교환법칙이 성립하지만, 사실 commutativity는 매우 특별한 특성이며
우리가 아는게 적어서 그렇지 실제로는 대부분의 행동그룹에서 commutativity가 성립되는 경우는 드물다고 한다.

2. Quaternion, Euler, Matrix변환

Using quaternions as rotations을 보면,
다음과 같이 표현되는 unit vector를 축으로 rotation of angle \(\theta\) 만큼 회전하는 경우,

\[{\displaystyle \mathbf {u} =(u_{x},u_{y},u_{z})=u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k} }\]

unit vector에 대해 \(\theta/2\)만큼 회전하는 quaternion number는 다음과 같다. \({\displaystyle \mathbf {q} =e^{ {\frac {\theta }{2}}{(u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k} )}}=\cos {\frac {\theta }{2}}+(u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k} )\sin {\frac {\theta }{2}}=\cos {\frac {\theta }{2}}+\mathbf {u} \sin {\frac {\theta }{2}}}\)

unit quaternion의 크기는 최대 1 radian이므로 90degree이고, 한쪽방향에서 양의 회전만으로 SO(3) group전체를 덮는 것은 불가능하다.(180degree가 필요하다.)
그래서 한 축방향으로 오른손법칙으로 \(\theta/2\)만큼 돌리고, 반대 축방향에서 왼손법칙으로 \(\theta/2\)만큼 한번더 돌리는 방식으로 총 \(\theta\)만큼의 회전을 정의한다.

회전이 pure queternion \({\displaystyle \mathbf {p'} }\)에 적용될 경우, q에 의한 \(p'\)의 congugation으로써 다음과 같이 나타난다.

\[{\displaystyle L(\mathbf {p'} ):=\mathbf {q} \mathbf {p'} \mathbf {q} ^{-1}=(0,\mathbf {r} ),}\] \[{\displaystyle \mathbf {r} =(\cos ^{2}{\frac {\theta }{2}}-\sin ^{2}{\frac {\theta }{2}}||\mathbf {u} ||^{2})\mathbf {p} +2\sin ^{2}{\frac {\theta }{2}}(\mathbf {u} .\mathbf {p} )\mathbf {u} +2\cos {\frac {\theta }{2}}\sin {\frac {\theta }{2}}(\mathbf {u} \times \mathbf {p} ),}\]

2.1. Quaternion, Euler, Matrix변환 in c code

mat2euler는 XYZ Euler angle을 기준으로 한다.
공식 은 다음과 같다.

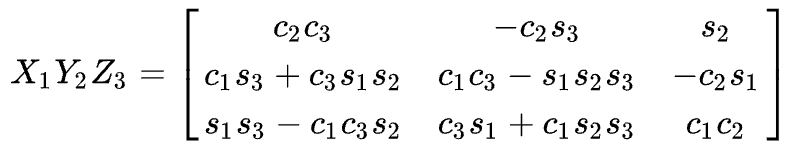
dircos[0]2의 절댓값이 1 근처(입실론:1e-15)인 경우, \(\theta_2=\phi/2 or -\phi/2\)를 의미하므로
th1,th2,th3를 구하는 방법이 달라짐을 볼 수 있다.
(singularity에 의해 th1과 th3이 겹쳐서 목표 orientation을 충족하는 {th1,th3}가 무한 개 존재하므로, th3를 0으로 두고 th1을 계산)

void mat2euler(double dircos[3][3],
    double *a1,
    double *a2,
    double *a3)
{
    double th1,th2,th3,temp[10];

    if (((fabs(dircos[0][2])-1.) <= -1e-15)  ) {
        th1 = atan2(dircos[2][1],dircos[1][1]);
        if ((dircos[0][2] > 0.)) {
            temp[0] = 1.5707963267949;
        } else {
            temp[0] = -1.5707963267949;
        }
        th2 = temp[0];
        th3 = 0.;
    } else {
        th1 = atan2(-dircos[1][2],dircos[2][2]);
        th2 = asin(dircos[0][2]);
        th3 = atan2(-dircos[0][1],dircos[0][0]);
    }
    *a1 = th1;
    *a2 = th2;
    *a3 = th3;
}

euler2mat는 a1,a2,a3를 각 축에 대한 회전행렬에 대입하고 3개의 행렬이 곱해진 공식을 따라 dircos에 대입한다.

void euler2mat(double a1,
    double a2,
    double a3,
    double dircos[3][3])
{
    double cos1,cos2,cos3,sin1,sin2,sin3;

    cos1 = cos(a1);
    cos2 = cos(a2);
    cos3 = cos(a3);
    sin1 = sin(a1);
    sin2 = sin(a2);
    sin3 = sin(a3);
    dircos[0][0] = (cos2*cos3);
    dircos[0][1] = -(cos2*sin3);
    dircos[0][2] = sin2;
    dircos[1][0] = ((cos1*sin3)+(sin1*(cos3*sin2)));
    dircos[1][1] = ((cos1*cos3)-(sin1*(sin2*sin3)));
    dircos[1][2] = -(cos2*sin1);
    dircos[2][0] = ((sin1*sin3)-(cos1*(cos3*sin2)));
    dircos[2][1] = ((cos1*(sin2*sin3))+(cos3*sin1));
    dircos[2][2] = (cos1*cos2);
}

quat2mat는 단순 계산이 너무 길다. 참고
vector v = Xi+Yj+Zk에 대해, rotation을 위한 unit quaternion곱을 취하면 Mv형태로 정리되고,
M이 곧 rotation matrix가 된다.

void quat2mat(double ie4, //constant
    double ie1, //qx
    double ie2, //qy
    double ie3, //qz
    double dircos[3][3])
{
    double e1,e2,e3,e4,e11,e22,e33,e44,norm;

    e11 = ie1*ie1;
    e22 = ie2*ie2;
    e33 = ie3*ie3;
    e44 = ie4*ie4;
    norm = sqrt(e11+e22+e33+e44);
    if (norm == 0.) {
        e4 = 1.;
        norm = 1.;
    } else {
        e4 = ie4;
    }
    norm = 1./norm;
    e1 = ie1*norm;
    e2 = ie2*norm;
    e3 = ie3*norm;
    e4 = e4*norm;
    e11 = e1*e1;
    e22 = e2*e2;
    e33 = e3*e3;
    dircos[0][0] = 1.-(2.*(e22+e33));
    dircos[0][1] = 2.*(e1*e2-e3*e4);
    dircos[0][2] = 2.*(e1*e3+e2*e4);
    dircos[1][0] = 2.*(e1*e2+e3*e4);
    dircos[1][1] = 1.-(2.*(e11+e33));
    dircos[1][2] = 2.*(e2*e3-e1*e4);
    dircos[2][0] = 2.*(e1*e3-e2*e4);
    dircos[2][1] = 2.*(e2*e3+e1*e4);
    dircos[2][2] = 1.-(2.*(e11+e22));
}

mat2quat는 주어진 mat의 요소 값을 quaternion q = e4 + e1i + e2j + e3k으로부터 matrix로 유도된 form의 matrix(quat2mat참고)의 각 요소와 비교해서 대수\ 계산한다. 참고
(계산상 테크닉을 보니 s,x,y,z중 tmp = (1./sqrt(((tmp1tmp1)+((tmp2tmp2)+((tmp3tmp3)+(tmp4tmp4))))))계산을 통해 약분할 term을 고르는 것같다.)

void mat2quat(double dircos[3][3],
     double *e4, //const
     double *e1, //qx
     double *e2, //qy
     double *e3) //qz
{
    double tmp,tmp1,tmp2,tmp3,tmp4,temp[10];

    tmp = (dircos[0][0]+(dircos[1][1]+dircos[2][2]));
    if (((tmp >= dircos[0][0]) && ((tmp >= dircos[1][1]) && (tmp >= dircos[2][2]
      )))  ) {
        tmp1 = (dircos[2][1]-dircos[1][2]);
        tmp2 = (dircos[0][2]-dircos[2][0]);
        tmp3 = (dircos[1][0]-dircos[0][1]);
        tmp4 = (1.+tmp);
    } else {
        if (((dircos[0][0] >= dircos[1][1]) && (dircos[0][0] >= dircos[2][2]))
          ) {
            tmp1 = (1.-(tmp-(2.*dircos[0][0])));
            tmp2 = (dircos[0][1]+dircos[1][0]);
            tmp3 = (dircos[0][2]+dircos[2][0]);
            tmp4 = (dircos[2][1]-dircos[1][2]);
        } else {
            if ((dircos[1][1] >= dircos[2][2])  ) {
                tmp1 = (dircos[0][1]+dircos[1][0]);
                tmp2 = (1.-(tmp-(2.*dircos[1][1])));
                tmp3 = (dircos[1][2]+dircos[2][1]);
                tmp4 = (dircos[0][2]-dircos[2][0]);
            } else {
                tmp1 = (dircos[0][2]+dircos[2][0]);
                tmp2 = (dircos[1][2]+dircos[2][1]);
                tmp3 = (1.-(tmp-(2.*dircos[2][2])));
                tmp4 = (dircos[1][0]-dircos[0][1]);
            }
        }
    }
    tmp = (1./sqrt(((tmp1*tmp1)+((tmp2*tmp2)+((tmp3*tmp3)+(tmp4*tmp4))))));
    *e1 = (tmp*tmp1);
    *e2 = (tmp*tmp2);
    *e3 = (tmp*tmp3);
    *e4 = (tmp*tmp4);
}