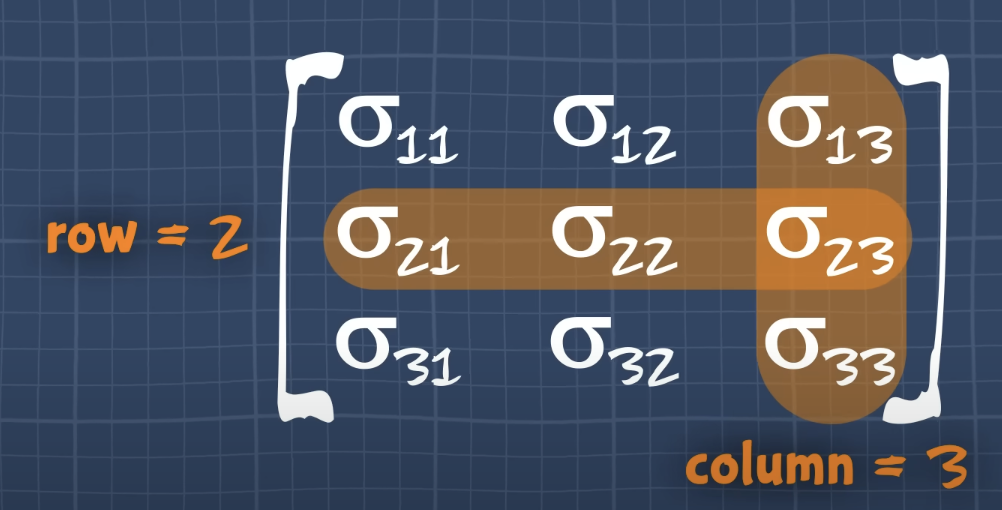개념-tensor
tensor의 수학적 정의는 “벡터 공간 및 그 쌍대공간들을 일종의 ‘곱연산’을 사용해 복합적으로 연결시킨 구조”이다. 선형대수학이 나오는 전반에서 사용되며, 미분기하학과 대수학에서 텐서서술이 약간 다르다. 이런 방식의 이해는 엄밀하지만 수학적 정의를 학습하는데 오래 걸린다..
필자는 로봇운동을 설명하기위한 고전역학에서 필요한 tensor만 알면된다.(지금은 moment of inertia tensor) 그래서 물리적 이해가 더 중요하다. 물리학에서는 자연현상을 설명하기 위해 거의 필수적으로 coordinate를 도입해서 시공간에 숫자를 부여하고 이 숫자들간의 관계로 법칙을 설명한다. 하지만 이렇게 coordinate, unit, measure를 도입하는 방법이 딱 한가지로 정해져 있는 것이 아니다. 그래서 coordinate와 무관하게 물리법칙을 기술할 필요성이 있어 tensor라는 개념이 도입된다.
tensor의 물리적 정의는 다음과 같다. A rank-n tensor in m-dimensions is a mathmatical object that has n indices and \(m^n\) components and obeys(coordinate와 무관하게) certain transformation rules.
stress tensor(m=3, n=2)
쉽게 말해, tensor는 transformation 중에도 그 의미를 유지하는 숫자(rank 0면 scalar) 또는 유사한 숫자의 모음(rank 1이면 벡터, rank 2면 행렬, rank 3이면 3차원행렬, …)이다.
if a real vector is zero in one set of coordinates, it must be zero in all of them.. 따라서 angular velocity는 사실 vector가 아닌 pseudo-vector이다.
w = r x v 이고 r은 좌표계의 원점에 의존한다.