article-imitation_learning

개요

RL은 policy를 따르는 agent가 environment과 상호작용하면서 최대의 누적 reward를 얻는 것이 목표이다.
agent는 environment에 대한 state를 갖고, policy에 기반하여 action하며, action의 결과로 reward를 받고 new state로 transition한다.
그러나 teaching process가 어렵고, 그래서 reward가 spase하거나 없는 경우가 있다. 이 경우 manually하게 rewards function를 설계할 수있는데,
rewards function를 설계하는 것은 복잡하다.
이 문제에 대한 feasible solution이 imitation learning(IL)이다. IL은 보상함수를 설계하는 것 대신, 인간같은 전문가가 set of demonstrations를
reward로 제공한다.

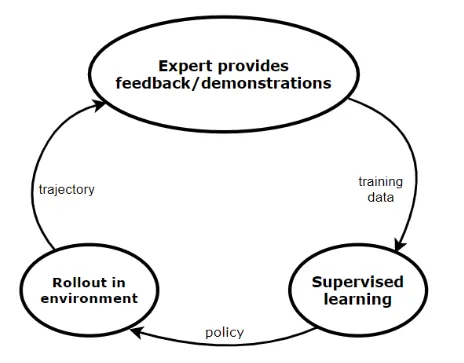
Behavioural Cloning(BC)

expert’s demonstrations이 주어졌을 때, supervised learning을 사용해서 expert’s policy를 학습하는 것이다. 알고리즘은 다음과 같다.

1. Collect demonstrations ($\tau^*$ trajectories) from expert
2. Treat the demonstrations as i.i.d. state-action pairs: $(s_0^, a_0^), (s_1^, a_1^), \ldots$
3. Learn $\pi_\theta$ policy using supervised learning by minimizing the loss function $L(a^*, \pi_\theta(s))$

Behavioural Cloning은 certain applications에서는 잘 작동하지만, 문제가 될 수 있다.
주된 이유는 i.i.d. assumption때문이다. supervised learning에서는 sample을 i.i.d.으로 간주하는 반면, MDP에서는 주어진 state내의 action이 다음 state를 유발하기 때문에, independent가 아니기 때문이다. 이는 expert와 다른 state에서 발생한 error가 누적됨을 의미한다. 그러므로 agent에 의해 발생한 실수(expert와 다른 state에 놓였기때문에 발생한 action)떄문에 expert가 겪지 못한 state로 transition하고, agent는 이 state에 대한 action을 train하지 못했기때문에 undefined action을 발생시킨다.

BC는 구현이 편하고 효율적이기때문에, 다음과 같은 조건에서는 사용할하다.

• long-term planning이 필요없는 경우
• expert’s trajectories가 state space전체를 cover할 수 있는 경우
• error를 저지르는 것이 치명적인 결과로 이어지지 않는 경우

Direct Policy Learning (via Interactive Demonstrator)

direct policy learning(DPC)는 BC의 개선된 버전이다. training time에 expert는 demonstrator(agent)와 interaction(query)할 수 있다. 알고리즘은 다음과 같다.

1. BC처럼 처음에 expert의 {state,action} pair(initial expert demonstrations)로부터 supervised learning한다.
2. 학습된 policy(initial predictor policy)에 기반하여 environment에서 action하는 것을 roll out(시연)하여 trajectory를 생성한다. 이를 이용해서 state distribution을 estimate한다.
3. 모든 state에 대해 expert는 demonstration을 제공하고, 이 feedback을 기반으로 agent는 new policy를 학습한다.
   이 loop는 converge할 때까지 계속된다.

DPL 알고리즘이 효율적으로 작동하기 위해서는, training동안 제공된 과거의 모든 data를 기억하고 있어야한다. 이러한 조건을 충족하는 알고리즘으로 다음의 2가지를 제시할 수 있다.

1. Data aggregation은 이전의 모든 training data에 대한 actual policy를 train한다.
2. policy aggregation는 직전 iteration에서 받은 training data에 대한 policy를 train하고
   이 policy를 이전의 모든 policy와 geometric blending한다. next iteration(roll out)에서 이 blended policy를 사용한다.

알고리즘은 다음과 같다.

Initial predictor: $\pi_o$
For m = 1:

• Collect trajectories $\tau$ by rolling out $\pi_{m-1}$
• Estimate state distribution $P_m$ using $s \in \tau$

• Collect interactive feedback ${ \pi^{*} (s)

  s \in \tau}$

• Data Aggregation (e.g. Dagger)
  • Train $\pi_m\ \text{on}\ P_1 \bigcup \cdots \bigcup P_m$
• Policy Aggregation (e.g. SEARN & SMILe)
  • Train $\pi^{‘}_m$ on $P_m$
  • $\pi_m = \beta \pi^{‘}m + (1-\beta)\pi{m-1}$

DPL은 BC의 단점을 극복한 효율적인 방법이다.
유일한 한계는 expert가 항상 agent의 action을 평가할 수 있어야하는 것이다.
이는 몇몇 application에서는 불가능하다.

Inverse Reinforcement Learning

inverse reinforcement learning(IRL)은 imitation learning의 다른 접근법이다.
expert’s demonstrations을 바탕으로 reward function을 학습하는 것이 목표이다. 그 후
학습한 reward function의 기반으로 RL을 수행하여 optimal policy를 찾는다.
즉, 다음과 같다.

We start with a set of expert’s demonstrations (we assume these are optimal) and then we try to estimate the parameterized reward function, that would cause the expert’s behaviour/policy.

IRL 알고리즘은 다음과 같다.

• Collect expert demonstrations: $D = {\tau_1, \tau_2, \cdots, \tau_m}$
• In a loop:
  • Learn reward function: $r_{\theta} (s_t, a_t)$
  • Given the reward function $r_{\theta}$, learn $\pi$ policy using RL
  • Compare $\pi$ with $\pi^*$ (expert’s policy)
  • STOP if $\pi$ is satisfactory

실제 문제에 따라, IRL은 2가지의 main approach가 존재한다.
바로 model-given, model-free approach이다.

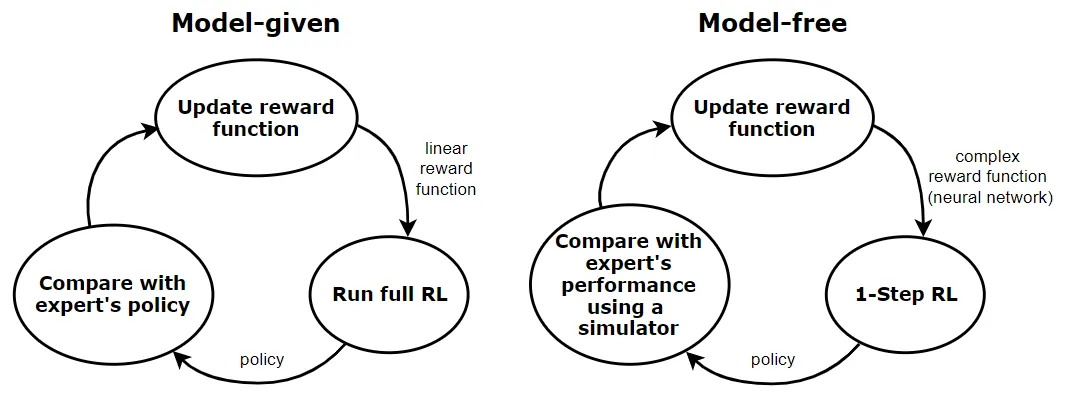
model-given case의 경우, reward function은 linear이다. 각 iteration마다 full RL problem을 푸는 것이 요구되며, MDP(environment)의 state space는 작다고 가정한다. 또 MDP의 state transition dynamics를 알고 있다고 가정한다(model given).

model-free approach의 경우, 더 일반적인 case이다. 여기서 reward function은 더 complex하다(보통 NN을 가진 model). 또 MDP의 state space는 크거나 continuous하다고 가정하고, 그래서 RL의 single step밖에 학습하지못한다. 또 MDP의 state transitions dynamics를 모르고, 그래서 우리는 simulator나 MDP(environment)에 access한다고 가정한다. 그래서 model-given case에 비해 policy를 expert’s policy와 비교하는 것이 비교적 어렵다.

두 경우 모두 reward function을 learning하는 것이 ambiguous하다. 많은 reward function이 같은 optimal policy(expert policy)에 이를 수 있기 때문이다. 이 문제를 해결하기 위해, maximum entropy principle(Ziebart)을 사용할 수 있다. 우리는 가장 큰 entropy를 갖는 trajectory distribution을 선택해야 한다.

참고자료

A brief overview of Imitation Learning