Mujoco-200-tutorials-Lec4:Double pendulum, modeling and control
Full code
1.Create a double pendulum model in xml
1
2
3
4
5
6
7
8
9
10
11
12
13
14
<mujoco>
<worldbody>
<light diffuse=".5 .5 .5" pos="0 0 3" dir="0 0 -1"/>
<geom type="plane" size="1 1 0.1" rgba=".9 0 0 1"/>
<body pos="0 0 3" euler="0 0 0">
<joint name="pin1" type="hinge" pos="0 0 -.5" axis="0 -1 0"/>
<geom type="cylinder" size=".05 .5" rgba="0 .9 0 1" mass="1"/>
<body pos="0 0.1 1" euler="0 0 0">
<joint name="pin2" type="hinge" pos="0 0 -0.5" axis="0 -1 0"/>
<geom type="cylinder" size=".05 .5" rgba="0 0 .9 1" mass="1"/>
</body>
</body>
</worldbody>
</mujoco>
2.Check energy balance of a free pendulum
1.timestep이 크면 오차가 누적되어 total energy가 줄어든다. 이번 case에서 timestep을 0.00005 하면 total energy변화가 충분히 적다.
2.integrator의 default는 euler method이다. 이 방법은 수치적분오차가 크므로 4차 Runge-Kutta(RK4)로 바꾸면 더 낫다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
<mujoco>
<option timestep="0.00005" integrator="RK4">
<flag energy="enable"/>
</option>
<worldbody>
<light diffuse=".5 .5 .5" pos="0 0 3" dir="0 0 -1"/>
<geom type="plane" size="1 1 0.1" rgba=".9 0 0 1"/>
<body pos="0 0 3" euler="0 0 0">
<joint name="pin1" type="hinge" pos="0 0 -.5" axis="0 -1 0"/>
<geom type="cylinder" size=".05 .5" rgba="0 .9 0 1" mass="1"/>
<body pos="0 0.1 1" euler="0 0 0">
<joint name="pin2" type="hinge" pos="0 0 -.5" axis="0 -1 0"/>
<geom type="cylinder" size=".05 .5" rgba="0 0 .9 1" mass="1"/>
</body>
</body>
</worldbody>
</mujoco>
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
// simulation end time
double simend = 2;
const int data_chk_period = 50; //frequency at which data is written to a file
void save_data(const mjModel* m, mjData* d)
{
//data here should correspond to headers in init_save_data()
//seperate data by a space %f followed by space
fprintf(fid,"%f, ",d->time);
fprintf(fid,"%f, %f, %f,",d->energy[0],d->energy[1], d->energy[0]+d->energy[1]);
//Don't remove the newline
fprintf(fid,"\n");
}
void my_controller(const mjModel* m, mjData* d)
{
//write control here
// Evaluate energy and store to data
mj_energyPos(m,d);
mj_energyVel(m,d);
printf("%f %f %f %f\n", d->time, d->energy[0], d->energy[1], d->energy[0]+d->energy[1]);
//write data here (dont change/dete this function call; instead write what you need to save in save_data)
if (loop_index%data_chk_period==0)
{
save_data(m,d);
}
loop_index = loop_index + 1;
}
int main() {
d->qpos[1] = 0.314;
while( !glfwWindowShouldClose(window)) {
if (d->time>=simend)
{
fclose(fid);
break;
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
clear all
clc
close all
filename = 'data.csv';
T = readtable(filename); %check T.Properties
VariableNames = T.Properties.VariableNames;
Arr = table2array(T);
[m,n] = size(Arr);
for i=2:n
figure(i)
% yy = i;
% plot(Arr(:,yy),'r');
% ylabel(cell2mat(VariableNames(yy)))
yy = i;
plot(Arr(:,1), Arr(:,yy),'r');
ylabel(cell2mat(VariableNames(yy)))
xlabel(cell2mat(VariableNames(1)))
end
3.Check equations of motion
dynamics \(\tau = M\ddot{q} + C + G\) M is 2x1 mass matrix, \(\ddot{q}\) is 2x1 acceleration vector, C is 2x1 coriolis force, G is 2x1 fravity force, \(\tau\) is external torque
in mujoco: qfrc_applied + ctrl = M\(\ddot{q}\) + qfrc_bias, qfrc_biased = C + G,
(d->qacc, d->qfrc_bias, d->qfrc_applied, d->ctrl)
ctrl is available on if actuator is defined (need to set actuator/motor tag in XML),
qfrc_applied is always available (general way)
So, \(\tau\) can be ctrl or qfrc_applied
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
void my_controller(const mjModel* m, mjData* d)
{
// Evaluate energy and store to data
mj_energyPos(m,d);
mj_energyVel(m,d);
// printf("%f %f %f %f\n", d->time, d->energy[0], d->energy[1], d->energy[0]+d->energy[1]);
// Check dynamics of motion
// M*qdotdot + qfrc_bias = qfrc_applied + ctrl
const int nv = 2;
double inertial_M[nv*nv] = {};
// matrix는 계산상 효율을 통해 sparse matrix로 변환되어 계산된다.(ex. d->qM)
// convert sparse inertia rank 2 tensor d->qM into full matrix(4 x 1) inertial_M.
mj_fullM(m, inertial_M, d->qM);
// 보기 편한 2 x 2 형태로 변환
double M[nv][nv] = {0};
M[0][0] = inertial_M[0];
M[0][1] = inertial_M[1];
M[1][0] = inertial_M[2];
M[1][1] = inertial_M[3];
// printf("%f %f\n", M[0][0], M[0][1]);
// printf("%f %f\n", M[1][0], M[1][1]);
// printf("******************\n");
double qacc[nv] = {0};
qacc[0] = d->qacc[0];
qacc[1] = d->qacc[1];
double qfrc_bias[nv] = {0};
qfrc_bias[0] = d->qfrc_bias[0];
qfrc_bias[1] = d->qfrc_bias[1];
// mju_mulMatVec(mjtNum* res, const mjtNum* mat, const mjtNum* vec, int nr, int nc);
double n_torque[nv] = {0};
mju_mulMatVec(n_torque, inertial_M, qacc, 2, 2);
double lhs[nv] = {0};
for(int i=0; i<nv; i++) {
lhs[i] = n_torque[i] + qfrc_bias[i];
}
// compensation with weight factor(.1, .5) for qfrc_bias(coriolis force, gravity force, etc.)
d->qfrc_applied[0] = 0.1*qfrc_bias[0];
d->qfrc_applied[1] = 0.5*qfrc_bias[1];
double rhs[nv] = {0};
for(int i=0; i<nv; i++) {
rhs[i] = d->qfrc_applied[i];
}
printf("%f %f\n", lhs[0], rhs[0]);
printf("%f %f\n", lhs[1], rhs[1]);
printf("******************\n");
//write data here (dont change/dete this function call; instead write what you need to save in save_data)
if (loop_index%data_chk_period==0)
{
save_data(m,d);
}
loop_index = loop_index + 1;
}
4.Torque-based position control using three method
4.1.position-derivative(PD) control
\[\tau = K_pq_{error} + K_d\dot{q_{error}}\]1
2
3
4
5
6
7
8
9
10
11
void my_controller(const mjModel* m, mjData* d) {
double kp1=400, kp2=300;
double kd1=500, kd2=500;
double qref1=-0.5, qref2=1.5;
// PD contorl
// $$\tau = K_pq_{error} + K_d\dot{q_{error}}$$
d->qfrc_applied[0] = kp1*(qref1 - d->qpos[0]) + kd1*(-d->qvel[0]);
d->qfrc_applied[1] = kp2*(qref2 - d->qpos[1]) + kd2*(-d->qvel[1]);
}
4.2.(gravity+coriolis forces)+PD control
\(\tau =\) qfrc_bias + \(K_pq_{error} + K_d\dot{q_{error}}\)
1
2
3
4
5
6
void my_controller(const mjModel* m, mjData* d) {
// (gravity+coriolis forces)+PD control
// $$\tau = $$ qfrc_bias + $$K_pq_{error} + K_d\dot{q_{error}}$$
d->qfrc_applied[0] = d->qfrc_bias[0] + kp1*(qref1 - d->qpos[0]) + kd1*(-d->qvel[0]);
d->qfrc_applied[1] = d->qfrc_bias[1] + kp2*(qref2 - d->qpos[1]) + kd2*(-d->qvel[1]);
}
4.3. PD feedback linearization control
\(\tau = M(K_pq_{error} + K_d\dot{q_{error}})\) + qfrc_bias
1
2
3
4
5
6
7
8
9
10
void my_controller(const mjModel* m, mjData* d) {
double n_torque[nv] = {0};
double pd_feedback[nv] = {0};
pd_feedback[0] = kp1*(qref1 - d->qpos[0]) + kd1*(-d->qvel[0]);
pd_feedback[1] = kp2*(qref2 - d->qpos[1]) + kd2*(-d->qvel[1]);
mju_mulMatVec(n_torque, inertial_M, pd_feedback, 2, 2);
d->qfrc_applied[0] = n_torque[0] + d->qfrc_bias[0] ;
d->qfrc_applied[1] = n_torque[1] + d->qfrc_bias[1];
}
5.Writing data file from Mujoco and plotting in MATLAB
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
clear all
clc
close all
filename = 'data.csv';
T = readtable(filename); %check T.Properties
VariableNames = T.Properties.VariableNames;
Arr = table2array(T);
[m,n] = size(Arr);
for i=2:n
figure(i)
% yy = i;
% plot(Arr(:,yy),'r');
% ylabel(cell2mat(VariableNames(yy)))
yy = i;
plot(Arr(:,1), Arr(:,yy),'r');
ylabel(cell2mat(VariableNames(yy)))
xlabel(cell2mat(VariableNames(1)))
hold on;
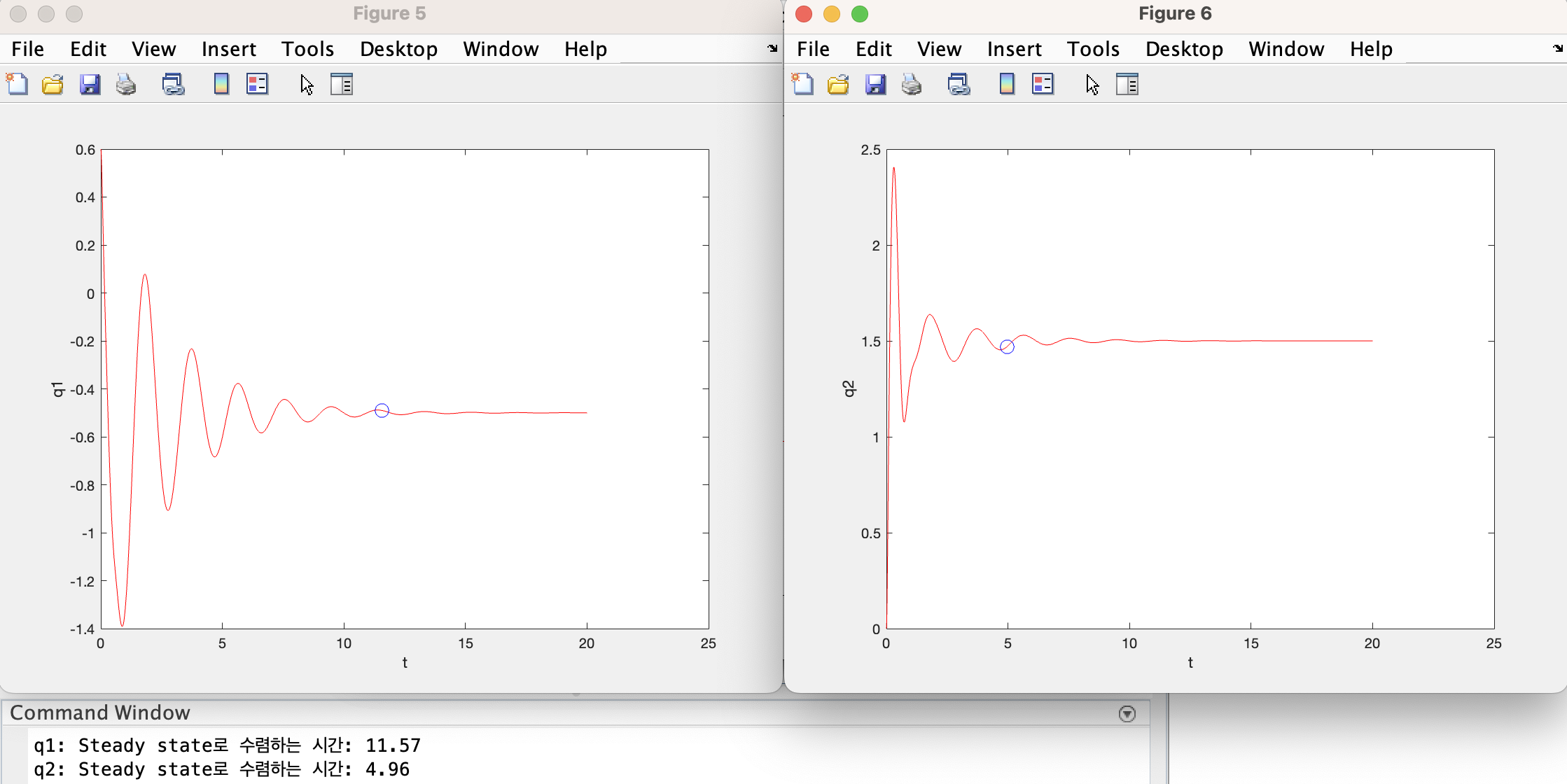
if(i==n-1 ||i==n)
% steady state로 수렴하는 시간 찾기
steady_state_value = Arr(m,i);
tolerance = abs(0.02*steady_state_value); % 수렴 허용 오차
index = find(abs(Arr(:,i) - steady_state_value) > tolerance, 1, 'last');
steady_state_time = Arr(index,1);
plot(steady_state_time, Arr(index,i), 'bo', 'MarkerSize', 10);
% 결과 출력
fprintf('q%d: Steady state로 수렴하는 시간: %.2f\n',i-(n-2), steady_state_time);
end
hold off;
end
6.각 제어 기법에 대한 비교
실험조건은 다음과 같다.
1
2
3
4
5
6
7
8
cylinder1, cylinder2의 mass="10"
double qref1=-0.5, qref2=1.5;
과감쇠
double kp1=400, kp2=300;
double kd1=500, kd2=500;
저감쇠
double kp1=200, kp2=100;
double kd1=10, kd2=10;
각 경우에 대해 수렴시간을 비교해보자.
| 과감쇠, PD | 과감쇠, bias+PD | 과감쇠, FB linearization | 저감쇠, PD | 저감쇠, bias+PD | 저감쇠, FB linearization | |
|---|---|---|---|---|---|---|
| q1 | 8.24 | 5.78 | 5.87 | 10.27 | 13.72 | 0.82 |
| q2 | 6.62 | 6.52 | 6.51 | 5.14 | 7.87 | 0.81 |
{과감쇠,bias+PD}는 {과감쇠,PD}보다 q1,q2의 수렴시간이 짧다. 과감쇠의 경우 중력이 감쇠작용을 돕지 않는다.
{저감쇠,PD}는 {저감쇠,bias+PD}보다 q1,q2의 수렴시간이 짧다. 저감쇠의 경우 중력이 감쇠작용을 돕는다.
PD, bias+PD 제어기는 dynamics equation을 몰라도 되는 제어기이다. 그래서 중력, 코리올리힘과 같은 qfrc_bias를 고려하면서 parameter를 튜닝해야한다.
반면 FB linearization제어기는 정확한 dynamics equation을 얻은 상태에서 error dynamics가 수렴할 때까지 진행되기 때문에, 모든 경우에 대해 수렴성이 양호하다!
즉, 과감쇠의 경우, 최소한 4.1.보단 수렴성 양호하고, 저감쇠의 경우, 최소한 4.2.보단 수렴성 양호하다.