Post

mujoco-200-tutorials-Lec6: Jacobian and its use for Inverse Kinematics

Posted
By
5 min read

lecture_url

docs

이번 시간에는 torque를 출력변수로하는 position control을 하려는 게 아니고, Jacobian과 Inverse Kinematics(IK)를 위한 Jacobian(여기서는 3D position에 대한)의 사용에 관심이 있다.

jacobian (jacobi matrix나 jacobi determinant를 총칭해서 부름):

다음과 같이 1차 편도함수로 구성된 행렬이다.

\[\mathbf {J} _{ij}={\frac {\partial f_{i}}{\partial x_{j}}}\] \[\mathbf {J} ={\begin{bmatrix}{\dfrac {\partial \mathbf {f} }{\partial x_{1}}}&\cdots &{\dfrac {\partial \mathbf {f } }{\partial x_{n}}}\end{bmatrix}}={\begin{bmatrix}\nabla ^{\mathrm {T} }f_{1}\\\vdots \\\nabla ^{\mathrm {T} }f_{m}\end{bmatrix}}={\begin{bmatrix}{\dfrac {\partial f_{1}}{\partial x_{1}}}&\cdots &{\dfrac {\partial f_{1}}{\partial x_{n}}}\\\vdots &\ddots &\vdots \\{\dfrac {\partial f_{m}}{\partial x_{1}}}&\cdots &{\dfrac {\partial f_{m}}{\partial x_{n}}}\end{bmatrix}}\]

Full code

test.cc
test.xml
xy_plot.m

Endeffector’s position and velocity(site,framepos,framelinvel)

jacobian에 joint angular velocity를 곱하여 얻은 end-effector의 linear velocity와 framelinvel를 비교해볼 것이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

<mujoco>
  <option timestep="0.00005" integrator="RK4" gravity="0 0 -1">
	<flag energy="enable" contact="disable"/>
  </option>
  
  <worldbody>
        <light diffuse=".5 .5 .5" pos="0 0 3" dir="0 0 -1"/>
    <geom type="plane" size="1 1 0.1" rgba=".9 0 0 1"/>
    <body pos="0 0 1.25" euler="0 90 0">
      <joint name="pin1" type="hinge" pos="0 0 -.5" axis="0 -1 0"/>
      <geom type="cylinder" size=".05 .5" rgba="0 .9 0 1" mass="1"/>
	  <body pos="0 0.1 1" euler="0 0 0">
		<joint name="pin2" type="hinge" pos="0 0 -.5" axis="0 -1 0"/>
		<geom type="cylinder" size=".05 .5" rgba="0 0 .9 1" mass="1"/>
		<site name="endeffector" pos="0 0 .5" size="0.1"/>
	  </body>
    </body>
  </worldbody>
  <actuator>
	<position name="pservo1" joint="pin1" kp="0"/>
	<velocity name="vservo1" joint="pin1" kv="0"/>
	<position name="pservo2" joint="pin2" kp="0"/>
	<velocity name="vservo2" joint="pin2" kv="0"/>
  </actuator>
  <sensor>
	<framepos objtype="site" objname="endeffector"/>
	<framelinvel objtype="site" objname="endeffector"/>
  </sensor>
</mujoco>

Get jacobian

아래 코드에서 jacobian은 jacp(3x2)이다.

각 row는 position x,y,z의 각 joint에 대한 gradient를 나타낸다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

void mycontroller(const mjModel* m, mjData* d)
{
	//write control here
	// printf("position = %f %f %f\n", d->sensordata[0], d->sensordata[1], d->sensordata[2]);
	// printf("velocity = %f %f %f\n", d->sensordata[3], d->sensordata[4], d->sensordata[5]);
	// mj_jac(const mjModel* m, const mjData* d, mjtNum* jacp, mjtNum* jacr, const mjtNum point[3], int body);
	double jacp[6] = {0};
	double point[3] = {d->sensordata[0], d->sensordata[1], d->sensordata[2]};
	int body = 2;
	mj_jac(m,d,jacp,NULL,point,body);	

	// printf("J = \n"); // 3x2
	// printf("%f %f \n", jacp[0], jacp[1]);
	// printf("%f %f \n", jacp[2], jacp[3]);
	// printf("%f %f \n", jacp[4], jacp[5]);
	// printf("******\n");

	double J[4] = {jacp[0], jacp[1], jacp[4], jacp[5]};
	double qdot[2] = {d->qvel[0], d->qvel[1]};
	double xdot[2] = {0};
	// void mju_mulMatVec(mjtNum* res, const mjtNum* mat, const mjtNum* vec, int nr, int nc);
	mju_mulMatVec(xdot,J,qdot,2,2);
	printf("velocity using jacobian(x,z): %f %f \n", xdot[0], xdot[1]);
	printf("velocity using sensor(x,z): %f %f \n", d->sensordata[3], d->sensordata[5]);
	

  //write data here (dont change/dete this function call; instead write what you need to save in save_data)
  if ( loop_index%data_chk_period==0)
    {
      save_data(m,d);
    }
  loop_index = loop_index + 1;
}

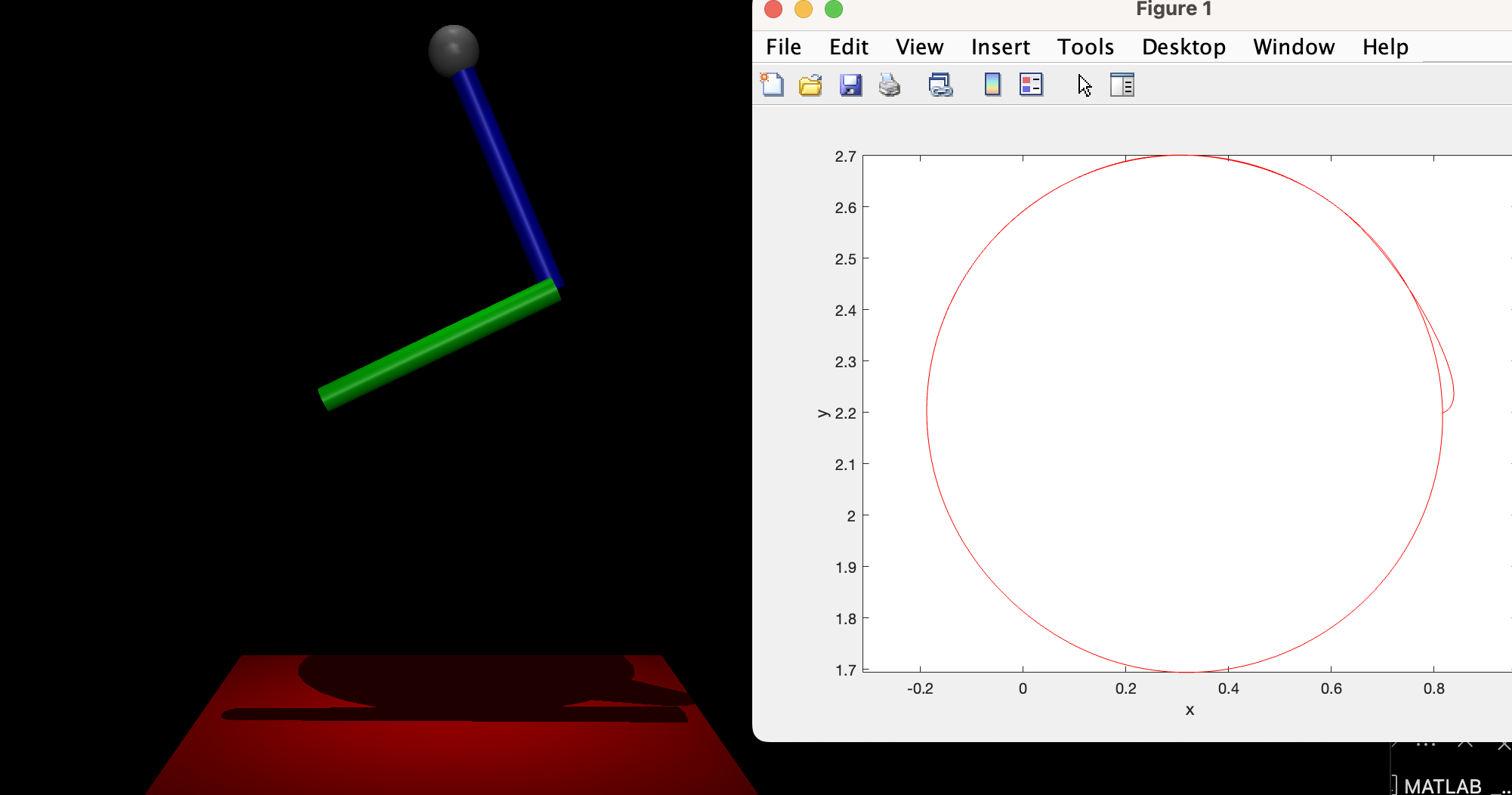
IK

이 방법은 position의 변화가 미소하다는 가정을 만족해야한다. 만약 position의 큰 변화에 대해 IK의 해를 구하고 싶다면, nonliner solver가 필요하다.

render and plot

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

void mycontroller(const mjModel* m, mjData* d)
{
	// write control here
	// printf("position = %f %f %f\n", d->sensordata[0], d->sensordata[1], d->sensordata[2]);
	// printf("velocity = %f %f %f\n", d->sensordata[3], d->sensordata[4], d->sensordata[5]);
	// mj_jac(const mjModel* m, const mjData* d, mjtNum* jacp, mjtNum* jacr, const mjtNum point[3], int body);
	double jacp[6] = {0};
	double point[3] = {d->sensordata[0], d->sensordata[1], d->sensordata[2]};
	int body = 2;
	mj_jac(m,d,jacp,NULL,point,body);	

	// printf("J = \n"); // 3x2
	// printf("%f %f \n", jacp[0], jacp[1]);
	// printf("%f %f \n", jacp[2], jacp[3]);
	// printf("%f %f \n", jacp[4], jacp[5]);
	// printf("******\n");

	double J[4] = {jacp[0], jacp[1], jacp[4], jacp[5]};
	double qdot[2] = {d->qvel[0], d->qvel[1]};
	double xdot[2] = {0};
	// void mju_mulMatVec(mjtNum* res, const mjtNum* mat, const mjtNum* vec, int nr, int nc);
	mju_mulMatVec(xdot,J,qdot,2,2);
	// printf("velocity using jacobian(x,z): %f %f \n", xdot[0], xdot[1]);
	// printf("velocity using sensor(x,z): %f %f \n", d->sensordata[3], d->sensordata[5]);
	
	// d->ctrl[0] = qinit[0];
	// d->ctrl[2] = qinit[1];

	double det_J = J[0]*J[3] - J[1]*J[2];
	double temp_J[4] = {J[3],-J[1],-J[2],J[0]};
	double inv_J[4] = {0};
	for(int i=0; i<4; i++) {
		inv_J[i] = temp_J[i]/det_J;
	}
	// trajectory in task space
	double x,y;
	x = x_0 + r*cos(omega*d->time);
	y = y_0 + r*sin(omega*d->time);
	// dq = Jinv*dr
	double dr[2] = {x-d->sensordata[0], y-d->sensordata[2]};
	double dq[2] = {};
	mju_mulMatVec(dq,inv_J,dr,2,2);
	// q = q+dq	// ctrl = q
	d->ctrl[0] = d->qpos[0] + dq[0];
	d->ctrl[2] = d->qpos[1] + dq[1];
	


  //write data here (dont change/dete this function call; instead write what you need to save in save_data)
  if ( loop_index%data_chk_period==0)
    {
      save_data(m,d);
    }
  loop_index = loop_index + 1;
}
mujoco
This post is licensed under CC BY 4.0 by the author.